Classification and reduction of Yutsis graphs

Classification and reduction of Yutsis graphs |
 |
HomeContentsAuthorsDries Van Dyck |
Project descriptionWe define a binary coupling tree on n+1 leaves as an unordered binary tree in which each leaf has a distinct label. A Yutsis graph of order n consists of two binary coupling trees on n+1 leaves, using the same label set, in which the unique leaves with the same label are identified. Note that both root nodes are also connected by an edge. The leaf nodes themselves disappear from the graph. The following figure shows an example of two binary coupling trees (a), the corresponding Yutsis graph of order 4 (b) and the same Yutsis graph redrawn (c). 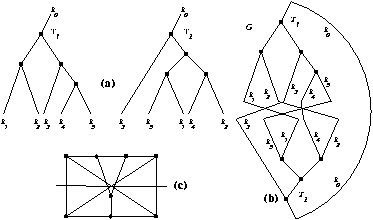 The motivation for this definition comes from theoretical physics. In the context of quantum theory of angular momentum Yutsis graphs are used to represent a 3nj-coefficient, while the binary coupling trees correspond to the coupling schemes in the bra/kets of the 3nj-coefficient (see [BL81] and [YLV62]). A Yutsis graph of order n is a cubic graph with 2n nodes and 3n edges, with the additional property that it contains an edge-cut on n+2 edges separating the graph into two vertex-induced trees of equal size. We call such a cut a defining cut of the Yutsis graph, the two trees are called defining trees of the Yutsis graph. By construction Yutsis graphs cannot contain a bridge. In this project we tackle two problems:
|